 | Deutsch
| English
| Deutsch
| English
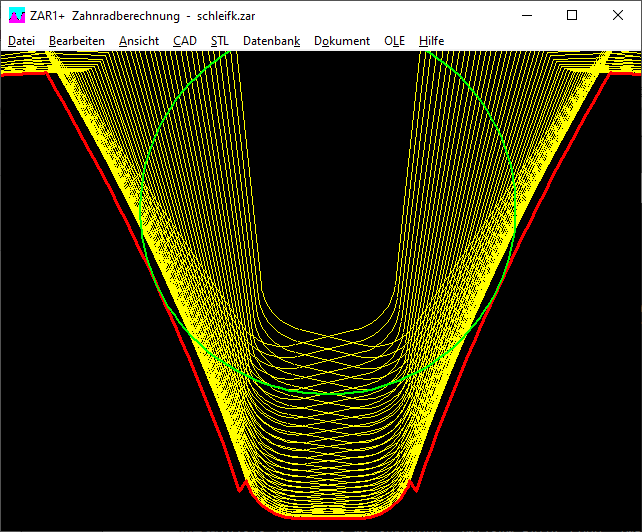
ZAR1+, ZAR5, ZAR7, ZAR8, ZAR1W: Schleifkerben durch Bearbeitungszugabe

Schon wieder hat ein Kunde ein Zahnprofilbild geschickt mit einem Zacken vom Übergang der Evolvente in die Zahnfußausrundung mit der Frage, ob das ein Fehler in der Software sei. Die Überprüfung seiner Berechnungsdatei ergab, dass eine Bearbeitungszugabe q eingegeben wurde, aber ein normales Bezugsprofil (kein Protuberanzprofil) verwendet wurde. Dann gibt es Schleifkerben, und diese sieht man auch im Zahnprofilbild.

Für unerfahrene Benutzer ist vielleicht auch nicht verständlich ,was "Bearbeitungszugabe q" bedeutet und sie klicken einfach auf den Vorgabebutton "<". Deshalb gibt es jetzt eine Änderung im Programm: nur wenn zuvor ein Protuberanzprofil definiert wurde, kommt ein Vorschlag für die Bearbeitungszugabe, andernfalls wird q=0 gesetzt. Auch der Vorschlag für die Bearbeitungszugabe wurde angepasst: 80% Bearbeitungszugabe plus 20% Toleranz, statt 50% + 50% wie bisher.
ZAR1+, ZAR5, ZAR7, ZAR8, ZAR1W: Formkreisdurchmesser dFf bei Protuberanz
Unter "CAD\Einstellungen" kann man jetzt "xev" ankreuzen, dann wird der Fußformkreisdurchmesser im Falle von Protuberanzprofil an der Stelle berechnet, wo die geschliffene Evolvente in die gefräste Evolvente übergeht. Wenn die Protuberanz nur teilweise weggeschliffen wurde, kann dieser Fußformkreisdurchmesser nur grafisch ermittelt werden durch Export in CAD und Ausmessen. Ansonsten ("xev" nicht angekreuzt) wird der Fußformkreisdurchmesser wie bisher an der Stelle berechnet, wo die Evolvente in die Fußausrundung übergeht.
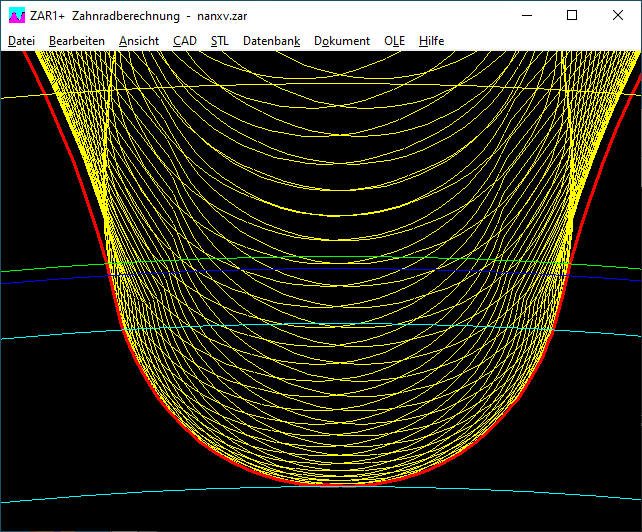
Dunkelblau: Fuß-Formkreisdurchmesser dFf
Grün: Fuß-Nutzkreisdurchmesser dNf (durch Gegenrad)
Hellblau: Grundkreisdurchmesser db und Fußkreisdurchmesser df
ZAR7, ZAR8: Export ZAR1
In ZAR7 und ZAR8 kann man jetzt ein Getriebepaar auswählen (Sonne-Planet, Planet-Planet, Planet-Hohlrad) auswählen und in ZAR1+ exportieren.
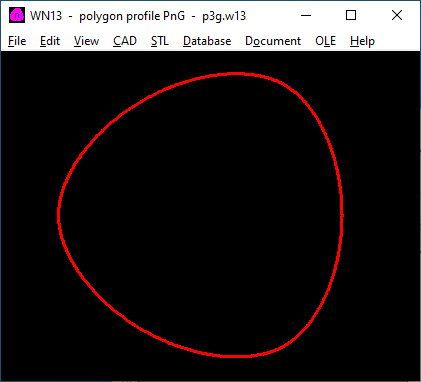
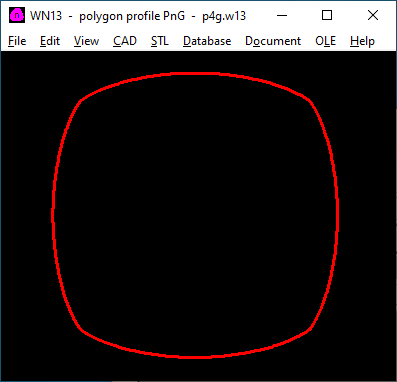
WN13: Software zur Berechnung von Welle-Nabe-Verbindungen mit PnG-Polygonprofil
Mit WN13 kann man P3G-Profile nach DIN 32711 berechnen, aber auch mit anderen Zähnezahlen (P2G, P4G, P5G, P6G). WN13 ersetzt somit WN6, Berechnung von Abmessungen und Profilkurve sind identisch. Flächenpressung und Mindestwanddicke werden aber nicht nach DIN 32711 berechnet, sondern nach DIN 6892 (Flächenpressung Paßfederverbindung) und DIN 7190 (Mindestwanddicke Preßverband). Dateien aus WN6 kann man importieren.
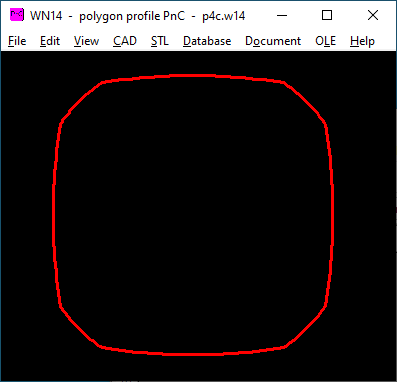
WN14: Software zur Berechnung von Welle-Nabe-Verbindungen mit PnC-Polygonprofil
Mit WN14 kann man P4C-Profile nach DIN 32712 berechnen, aber auch mit anderen Zähnezahlen (P2C, P3C, P5C, P6C). WN14 ersetzt somit WN7, Berechnung von Abmessungen und Profilkurve sind identisch. Flächenpressung und Mindestwanddicke werden aber nicht nach DIN 32712 berechnet, sondern nach DIN 6892 (Flächenpressung Paßfederverbindung) und DIN 7190 (Mindestwanddicke Preßverband). Dateien aus WN7 kann man importieren.
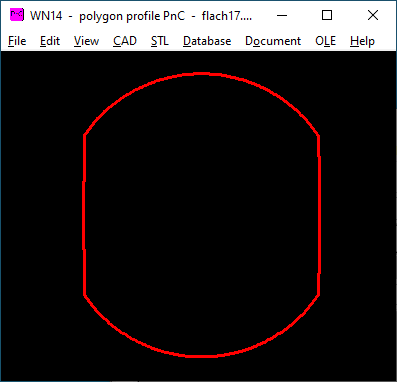
Man kann auch eine angeflachte Welle berechnen: Außendurchmesser eingeben, Innendurchmesser=Schlüsselweite, Exzentrizität ist theoretisch unendlich groß, es reicht aber auch e=1000mm.
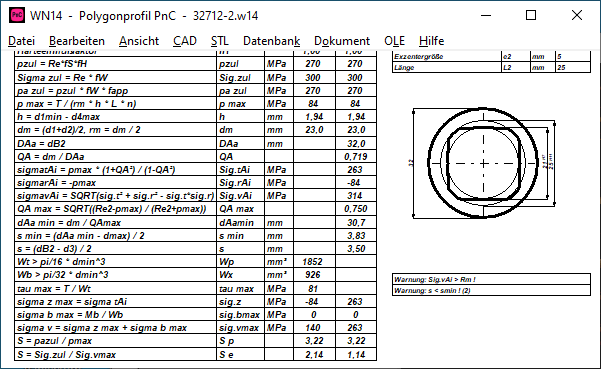
WN13, WN14: Flächenpressung PnG und PnC
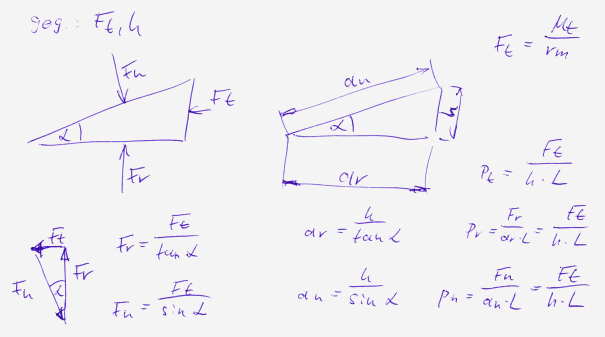
Wie verteilt sich die Flächenpressung über ein Gleichdick-Profil? Am Größt- und Kleinstdurchmesser dürfte die Flächenpressung durch Radialkraft am höchsten und durch Tangentialkraft am niedrigsten sein, in der Mitte gibt es Flächenpressung durch Tangentialkraft und durch Radialkraft.
Betrachten wir die Flächenpressung auf einen Keil. Man könnte erwarten, dass die Flächenpressung dort am höchsten ist, wo die Kraft am größten ist. Tatsächlich sind aber Kraft und Auflagefläche proportional, weshalb die Flächenpressung am Keil überall gleich groß ist: p=Ft/(h*L)
Mit dieser Erkenntnis kann man auch für PnG und PnC Profile die Flächenpressung gleich wie für andere Vielzahnprofile aus Drehmoment, mittlerem Durchmesser, Länge, Zahnhöhe und Zähnezahl berechnen:
P = F/A = T/(rm*L*h*n)
Wenn man die Durchmesserbezeichnungen aus DIN 32711 und 327122 verwendet, ist der mittlere Radius rm bei PnG: rm = d1/2 und bei PnC: rm = (d1+d2)/4.
Bei einer Presspassung erhöht sich die Flächenpressung um
p = Pu – f*(Rz1+Rz2)* Elastizitätsmodul / (dm * Qk)
Das wird in WN6, WN7, WN13 und WN14 vorerst nicht berücksichtigt, in DIN 32711 und 32712 auch nicht.
WN13, WN14: Kleinste Nabenwanddicke berechnen
In DIN 32711 und 32712 gibt es eine einfache Näherungsformel zur Abschätzung der erforderlichen Nabenwanddicke:
s = f * SQRT(Mt / (Sigma z,zul * L))
mit
Sigma z,zul = Re
L = Nabenlänge
Mt = Drehmoment
f = Anwendungsfaktor:
f = 1.44 für P3G mit d4 <= 35mm
f = 1.2 für P3G mit d4 > 35mm
f = 0.7 für P4C
Merkwürdigerweise ist in dieser Formel die Mindestwanddicke nur von der Nabenlänge abhängig, der Durchmesser bleibt unberücksichtigt.
In WN13 und WN14 wird die Mindestwanddicke dagegen von den Formeln für Spannungen im Preßverband abgeleitet. Die größte Tangentialspannung tritt an der Innenseite der Nabe auf:
Sigma tAi = p * (1 + QA²/(1-QA²)
Mit QA = Außendurchmesser Nabe dAa / Fügedurchmesser dm.
Mit Begrenzung der maximalen Tangentialspannung auf die Streckgrenze (Sigma tAi = Re) und Umstellung der Formel auf QA ergibt sich:
QA = SQRT((Re+p)/(Re-p))
Mit QA = dm/DaA und Wanddicke s = (DaA – dm)/2 wird die Mindestwanddicke
smin = dm/2 * (SQRT((Re+p)/(Re-p)) – 1)
Mit dieser Formel muss die Flächenpressung pmax kleiner als die Streckgrenze Re sein, sonst wird die Wanddicke unendlich groß. Beim Preßverband (Berechnung mit WN1) darf die Streckgrenze durchaus überschritten werden, man spricht dann vom elastisch-plastischen Spannungszustand mit teilplastischer Verformung. Da PnG und PnC Verbindungen eher als lösbare Verbindungen verwendet werden, ist die Begrenzung der Fächenpressung auf die Streckgrenze Re sinnvoll.
Zwar ist die zulässige Flächenpressung auch nach DIN 6892 höher als die Streckgrenze (pzul=Re*fS*fH), weil eine Druckspannung höher sein darf als eine Zugspannung. Weil aber bei der Nabe die Flächenpressung eine mindestens gleich große Zugspannung erzeugt, muß zumindest bei der Nabe die Flächenpressung kleiner als die Streckgrenze des Werkstoffs sein.
Beim Vergleich der berechneten Mindestwanddicke mit DIN 32711 und DIN 32712 anhand der Berechnungsbeispiele im Anhang A (P3G und P4C mit Nennmaß 25mm und Drehmoment 150 Nm) sind die Ergebnisse erstaunlicherweise fast identisch: s= 7.0mm (7.2 nach DIN) bei P3G und 3.8mm bei P4C (3.5mm nach DIN). Das liegt aber auch daran, dass in WN13 mit pmax = 126 statt 96 MPa und in WN14 mit pmax= 84 statt 51 MPa gerechnet wurde. Oder es ist Zufall, weil bei der DIN-Näherungsformel ein Durchmesser (Hebelarm) und damit Tangentialkraft und Flächenpressung gar nicht berücksichtigt sind.
WN13, WN14: Aufweitung berechnen
Mit den Formeln aus der Berechnung von Preßverbänden wird in WN13 und WN14 die maximale Aufweitung der Nabe am Außendurchmesser berechnet. Das ist wichtig wenn die Nabe z.B. ein Zahnrad ist.
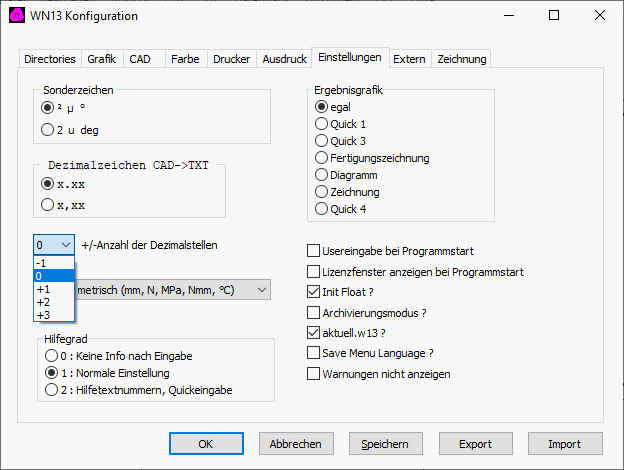
Alle Programme: Einstellungen Dezimalstellen
Bei der Einstellung wurde die Anzeige geändert: statt 2,3,4,5 steht jetzt –1,0,+1,+2. Standardeinstellung ist 0. Mit "-1" werden Zahlen mit 1 Dezimalstelle weniger angezeigt, mit "+1" mit einer Dezimalstelle mehr. Bei der alten Darstellung hatten sich Anwender beschwert, dass Zahlen nicht mit der gewählten Zahl Dezimalstellen angezeigt wurde. Es macht aber keinen Sinn, große Zahlen mit 2 bis 5 Dezimalstellen auszugeben (F = 9567,567 N).
Rechnung für Wartungsverträge mit 19% Mwst.
Komischerweise fällt auf Rechnungen von Software-Wartung 19% Mwst. an, weil das "Ende des Leistungszeitraums" 2021 ist. Darauf wurden wir von Kunden aufmerksam gemacht, und die Rechnungen mussten geändert werden.
Coronatest statt Volksfest: Wasenhelfer gesucht - gefunden
Können sich vormals Gesunde beim Corona-Test mit dem Virus infizieren? Sehr wahrscheinlich, wenn man sieht, wie die Helfer mit ihren Gummihandschuhen den Menschen ins Gesicht fassen. Die Stadt Stuttgart braucht neue Helfer für das neue Corona-Testzentrum auf dem Cannstatter Wasen und ruft vor allem Studierende auf, sich zu bewerben. Mindestanforderungen: keine. Sinnvoller wäre es, Roboter auf Corona-Tests zu programmieren. Dann sitzt jeder Griff, und Kollege Roboter könnte sich nach jedem Abstrich zuverlässig selbst desinfizieren.
Recht auf Homeschooling statt Recht auf Homeoffice !
Wie erwartet, haben Reisende das Coronavirus aus Risikoländern zurückgebracht. Danach wurde es über Schule, Kindergarten, Arbeitsstätte und private Feiern großflächig verbreitet. Schüler können sich nicht gegen eine Ansteckung schützen, sie werden gezwungen den Präsenzunterricht zu besuchen. Der Mindestabstand kann nicht eingehalten werden, weil die Klassenzimmer zu klein sind. Masken schützen nicht, wenn man stundenlang zusammensitzt. Deshalb sollten die zuständigen Politiker besser für Schüler statt für Arbeiter ein Recht auf Homeoffice fordern. Wer Präsenzunterricht will geht in die Schule. Und wer zuhause bleiben will, muss Homeschooling machen. Der Aufwand wäre überschaubar: Aufgaben und Arbeitsblätter ins Netz stellen, und der Lehrer bekommt ein Mikrofon und eine Kamera.
Für Betriebe dagegen braucht es kein Recht auf Homeoffice von Amts wegen. Ein Unternehmer hasst nichts mehr als überflüssige Vorschriften durch inkompetente Beamte und Politiker.
Mautpreller
Was der deutsche Verkehrsminister für ein Typ ist, sieht man allein schon an der Begründung und dem Zeitpunkt seiner gekündigten Mautverträge: Begründung: Qualitätsmängel von Seiten der Lieferanten, Zeitpunkt: sofort nachdem die Gerichte seine Mautpläne ablehnten. Qualitätsmängel an Produkten, die noch nicht geliefert wurden und auch nicht mehr gebraucht werden. Das glatte Gegenteil eines "ehrbaren Kaufmanns". Dem würde ich keine Software verkaufen.