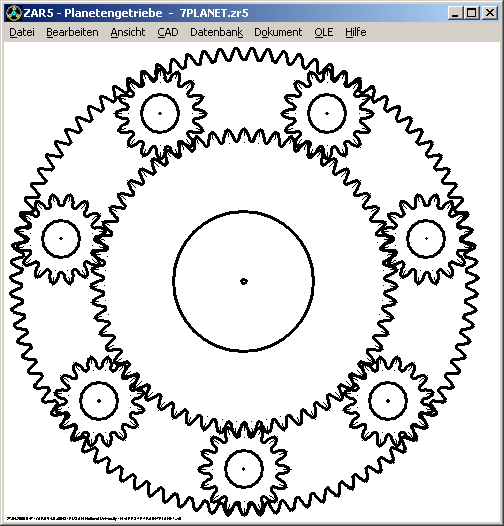

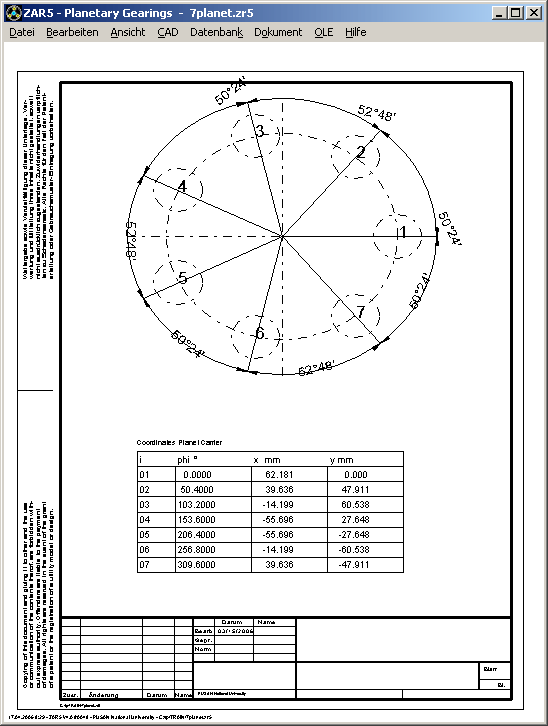
Für Planetengetriebe gilt die Montierbarkeitsbedingung:
(zH+zS) / qp muß ganzzahlig sein !
(zH und zS = Zähnezahl Hohlrad und Sonnenrad, qp=Anzahl Planeten).
Der Winkel für die Anordnung der Planeten auf dem Planetenträger ist 360°/qp. Wenn man die Zähnezahlen von Hohlrad oder Sonnenrad nicht verändern will oder kann, oder nachträglich die Zahl der Planeten verändert wird, kann man die Montierbarkeit durch ungleiche Planetenwinkel auf dem Planetenträger erreichen. In der neuen Version 4.0 von ZAR5 werden in diesem Fall die einzelnen Planetenwinkel und Koordinaten auf dem Planetenträger berechnet nach folgender Formel:
Planetenwinkel i = round [i / qp * (zH + zS)] * 360° / (zH + zS)
mit i = 0 .. qp-1
round() : runden auf die nächste ganze Zahl
Die Fehlermeldung "nicht montierbar !" wurde ersetzt durch die Warnung "unsymmetrisch !".
Ein Bohrbild mit Koordinaten und Winkel der Planeten auf dem Carrier kann man als Fertigungszeichnung ausgeben.
ZAR3 - Vorauslegung
Für die Vorauslegung (Berechnung der Abmessungen aus Leistungs- und Werkstoffdaten) gibt es ein neues, komfortableres Eingabefenster. Außerdem kann man jetzt wahlweise Antriebs- oder Abtriebsleistung eingeben.
ZAR3 alphan, alphax = f (Profilform)
Die gebräuchlichsten Profilformen bei Schneckenradverzahnungen sind ZI, ZA, ZN und ZK-Schnecke. Bei der ZA-Schnecke liegt der Erzeugungs-Eingriffswinkel im Axialschnitt (alpha 0 = alpha x). Bei ZI-, ZN und ZK-Schnecke liegt der Erzeugungs-Eingriffswinkel in einer Ebene, die zur Schneckenachse um den Mittensteigungswinkel gamma m geneigt ist (alpha 0 = alpha n). In ZAR3 wurde bisher fälschlicherweise für alle Profile mit alpha x = alpha 0 gerechnet. Das wurde jetzt korrigiert, in Ausdruck und Tabellen werden Erzeugungs-, Normal- und Axialeingriffswinkel alpha 0, alpha n und alpha x ausgegeben.
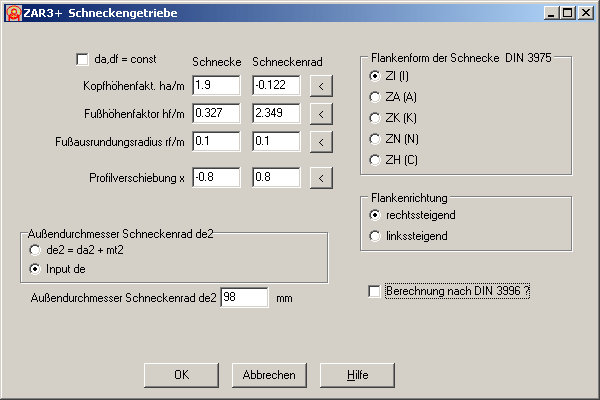
Der Außendurchmesser de2 des Schneckenrads wird ermittelt aus dem Kopfkreisdurchmesser in der Hohlkehle und dem Modul (de2 = da2+mt2). Alternativ kann man de2 jetzt auch manuell eingeben.
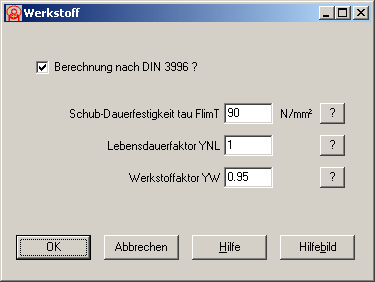
Bei Berechnung nach DIN 3996 werden zusätzliche Werkstoffeingaben benötigt (tauFlimT, YNL, YW). Diese wurden in einem Fenster zusammengefaßt.
ZAR3 - Export ZAR1
Die ZI-Schnecke kann man auch in ZAR1+ darstellen. Im Radialschnitt ist die Schnecke eine Zahnstange, das Schneckenrad wird als schrägverzahntes Stirnrad (beta = gamma m) in der Hohlkehle dargestellt.
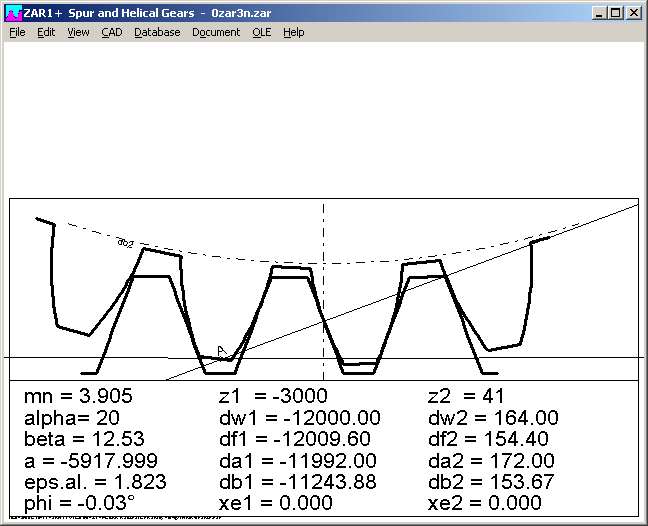
Wenn man die ZI-Schnecke im Stirnschnitt darstellen will, kann man in ZAR1+ die Gangzahl als Zähnezahl z1 eingeben (muß größer als 1 sein), der Schrägungswinkel ist dann beta = 90° - gamma_m.
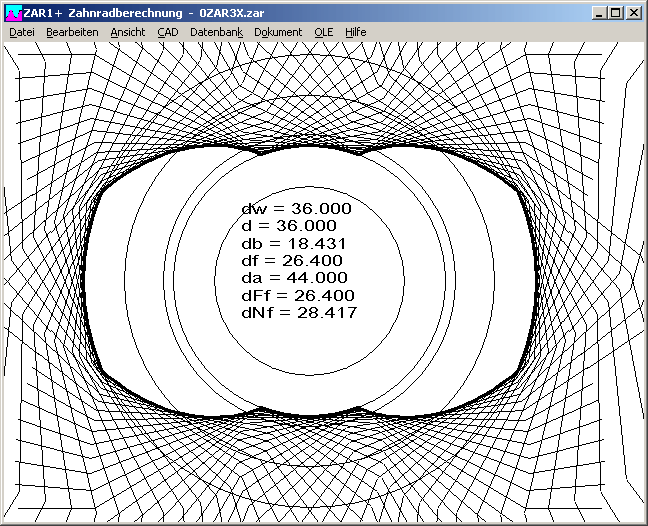
In das Eingabefenster wurde der Steigungswinkel der Schnecke gamma_m (=Schrägungswinkel ß des Schneckenrads) aufgenommen. Bei Eingabe von gamma_m werden dm1, dm1/a und Modul m neu berechnet.
Demnächst gibt es von ZAR3 eine erweiterte Version ZAR3+ mit freidefinierbaren Zahnhöhenfaktoren und Profilverschiebungsfaktoren, Eingabe von Toleranzen, Berechnung von Prüfmaßen, Zahnformzeichnungen von Schnecke und Schneckenrad am Bildschirm oder als CAD-Datei
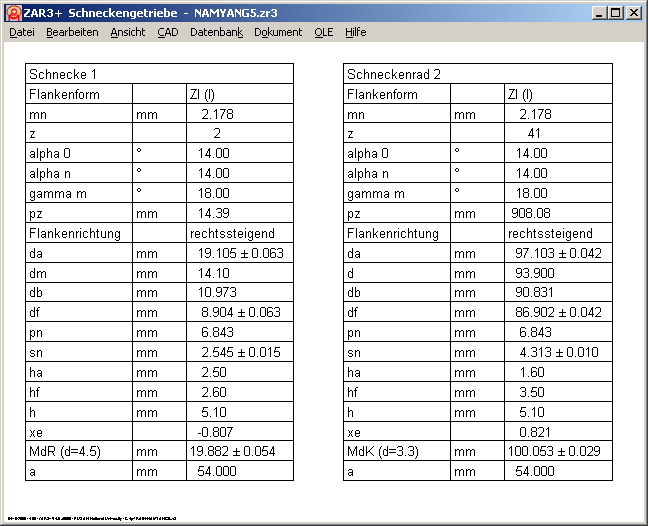
ZAR1+ Eingabefenster für Berechnung nach DIN 3990 Teil 1-3
Die Einzeleingaben für Ritzellagerung und Zahnkorrekturen wurden in einem Fenster zusammengefaßt. Das erhöht die Übersichtlichkeit und beschleunigt die Eingabe. Mit einem Mausklick auf die ? - Buttons werden die zugehörigen Hilfebilder angezeigt.
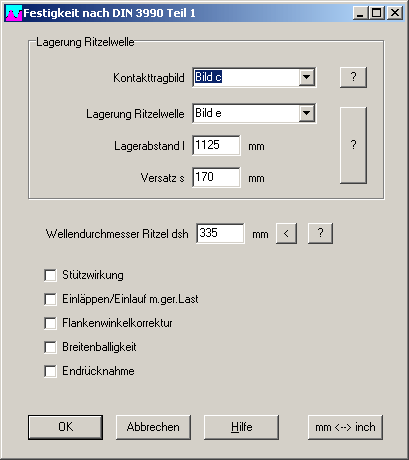
ZAR1+ Achsabstand Zahnstange
Unter "Sonderabmessungen->Zahnstange-Ritzel" kann man jetzt die Höhe der Zahnstange (vom Rücken der Zahnstange bis Kopflinie) eingeben. ZAR1+ gibt dann im Ausdruck den Abstand vom Zahnrücken zur Ritzelachse (h-a) mit aus (h-a = a - da2 / 2 + h-da).

----------------------------------------------------------------------
Achsabstand a mm -2469.000
----------------------------------------------------------------------
Achsabstand - Teilkreisdurchm.2/2 a-r2 mm 31.000
----------------------------------------------------------------------
Höhe Zahnstange h-da mm 10.000
----------------------------------------------------------------------
Zahnstange Achsabstand h-a mm 38.806
----------------------------------------------------------------------
ZAR1+ Kv, KFalpha, KHalpha, KFß, KHß
Der Einlaufbetrag yp (yf, yalpha) war bisher nach DIN 3990 Teil 1 Methode C berechnet worden, die weiteren Faktoren für Kv dagegen nach der genaueren Methode B. Bei Berechnung nach DIN 3390 Teil 41 wurde der Einlaufbetrag zwar nach Methode B berechnet, jedoch unter der Voraussetzung (gemäß DIN 3990 Teil 41), dass die Zahnräder einsatzgehärtet oder nitriert sind.
Der Einlaufbetrag wird außerdem verwendet bei der Berechnung der Lastverteilungsfaktoren KFalpha, KHalpha, KFß, KHß nach Methode C2.
Die Berechnung des Einlaufsbetrags wurde überarbeitet und vollständig an Methode B angepasst. Für vernünftig dimensionierte Getriebe ergeben sich kaum Unterschiede zwischen der bisherigen und der neuen Berechnung. Größere Unterschiede gibt es bei schnelllaufenden Getrieben mit niedriger Belastung (Warnung Ft/b*KA < 100). Im konkreten Fall hatte ein Kunde festgestellt, daß die Sicherheiten besser (größer) werden, wenn die Verzahnungsqualität verschlechtert (erhöht) wird. Der Dynamikfaktor Kv war 3,7 bei Qualität 8 und 3,2 bei Qualität 9. Mit der genaueren Methode B ist nun Kv=6,3 bei Qualität 8 und Kv=8,1 bei Qualität 9!
ZAR1+ und ZAR5 benutzen denselben Berechnungskern, die genauere Berechnungsmethode wurde auch in die Festigkeitsberechnung der Planetengetriebe übernommen.
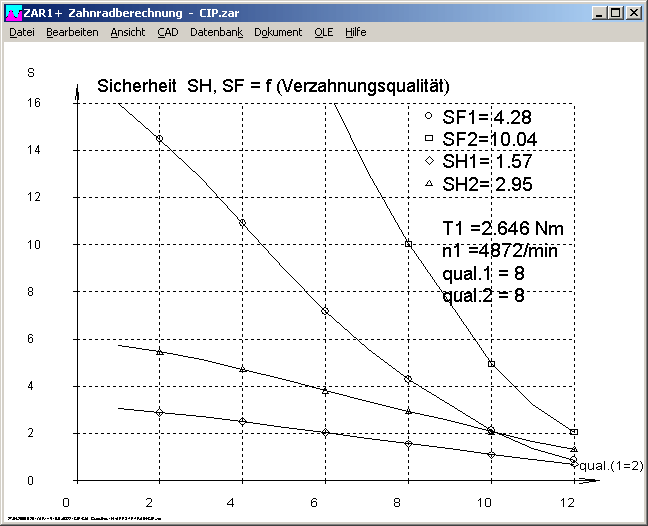
ZAR1+ Sicherheit = f (Verzahnungsqualität)
Neben einem Diagramm mit der Sicherheit als Funktion des Antriebsdrehmoments gibt es jetzt ein zweites Diagramm mit der Sicherheit in Abhängigkeit von der Verzahnungsqualität (bei gleicher Verzahnungsqualität für Rad1 und Rad2).
TOL1, TOL2 - Max. Anzahl der Elemente erhöht
Die maximale Anzahl der Maßelemente für eine Toleranzrechnung mit TOL1 wurde erhöht von 1000 auf 2500, die maximale Anzahl der kritischen Abstände von 100 auf 250.
In TOL2 kann man jetzt bis zu 200 Einzelteile (TOL1-Dateien) erfassen. Die maximale Anzahl der Maßlemente wurde von 1000 auf 2500 erhöht, die maximale Anzahl der kritischen Abstände von 100 auf 250.
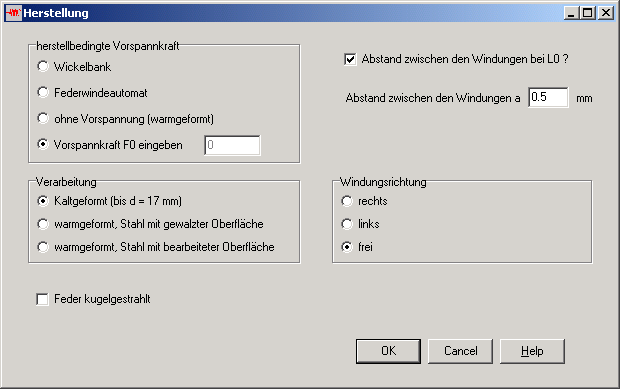
FED2+ Zugfeder mit Windungsabstand bei L0
Normalerweise werden Zugfedern mit anliegenden Windungen gewickelt, kaltgeformte Federn mit Vorspannung tau0 zwischen den Windungen, so daß sich die Feder erst bewegt, wenn die Zugkraft größer als F0 ist. Zugfedern mit Abstand zwischen den Windungen konnten bisher mit FED2+ nicht direkt berechnet werden. Um auch diesen Fall abzudecken, kann man jetzt unter "Bearbeiten->Herstellung" einen Windungsabstand a eingeben. Die Vorspannkraft F0 wird in diesem Fall auf 0 gesetzt. Die Länge des Federkörpers LK und sämtliche Federlängen erhöhen sich dann um n * a (Windungszahl * Windungsabstand).
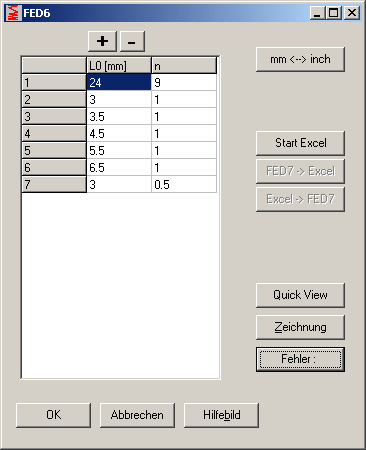
FED6 - Eingabe der progressiven Federkennlinie
Geben Sie bei der Eingabe der Federkennlinie nur die Knickpunkte ein (da wo sich die Federrate ändert). Die Eingabe von Zwischenpunkten gleicher Federrate kann bei der Berechnung Fehler verursachen. Wenn die berechnete Federrate nur um einige hundertstel kleiner (statt größer) als im Vorgängerabschnitt ist, erhalten Sie veränderte Kräfte oder Federlängen.
Für die Eingabe der Windungsabschnitte kann man wählen unter: Standard, Tabelle, Excel.
Bei Eingabe der Windungsabschnitte (unter "Tabelle" und "Excel") kann man jetzt auf Knopfdruck die Quick-Ansicht oder eine Federzeichnung anzeigen lassen. Bei der Eingabe der Federkennlinie ist das nicht möglich, hier muß zuerst eine Berechnung durchgeführt werden.