Infobrief Nr. 179 - Jan./Feb. 2020

von Fritz Ruoss

Wenn eine Zugfeder bricht, dann bricht sie meistens im Übergang von Federkörper in die Öse, dort wo die Torsionsspannung in eine Biegespannung übergeht.

Torsionsspannung im Federkörper: tau = Mt/Wt = F*Dm/2/(pi/16*d³)

Biegespannung am Ösenübergang: Sigmab = Mb/Wb = F*Dm/2/(pi/32*d³)

Zugspannung Öse: Sigma = F/A = F/(pi/4*d²)

Die Zugspannung ist vernachlässigbar klein, nur bei kleinem Wickelverhältnis Dm/d ist ihr Anteil relevant. Wichtiger ist die Kerbwirkung durch Abbiegeradius und Wickelverhältnis.

Die Biegespannung ist doppelt so groß wie die Torsionsspannung, dafür ist die zulässige Biegespannung im allgemeinen Maschinenbau auch etwa doppelt so groß wie die zulässige Torsionsspannung. Aber bei der Federberechnung nach EN 13906 ist es etwas anders: tau zul = 56% Rm bei Druckfedern und 45% Rm bei Zugfedern, Sigmabzul = 70% Rm bei Schenkelfedern. Die Beanspruchung von Zugfedern beim Übergang vom Federkörper in die Öse ist vergleichbar mit Schenkelfedern im Übergang von Federkörper zu Schenkel und wird in FED2+ auch so berechnet.

Um Biege- und Torsionsspannung im Ösenübergang zu verringern, kann man Ösendurchmesser und Windungsdurchmesser am Ösenübergang verringern ("eingezogene" Windungen), dadurch verringert sich der Hebelarm DmÖse/2. In FED2+ kann man jetzt bei den Ösen einen kleineren Windungs- und Ösendurchmesser bei eingezogenen Windungen durch Eingabe eines Faktors DmLoop/Dm eingeben. Bei der Berechnung der Biegespannung wird dann der Ösendurchmesser berücksichtigt.

Versuchsweise kann man auch eine Vergleichsspannung bei Federkraft F2 berechnen, wenn man unter Bearbeiten\Berechnungsmethode den entsprechenden Haken setzt. Versuchsweise, weil es keine gesicherte Berechnung für die größte Vergleichsspannung im Ösenübergang gibt, und die Berechnung der Vergleichsspannung noch verifiziert und verändert werden muss. Die Vergleichsspannung im Ösenübergang Sigmav2loop muss kleiner sein als die Zugfestigkeit Rm.

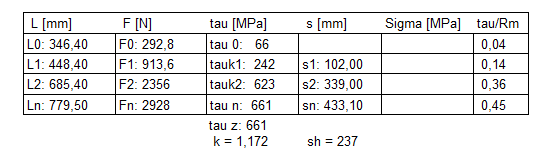
In der Tabelle in der Quick3-Ansicht wird die Biegespannung Sigma in der Öse nur noch angezeigt, falls eine Öse gewählt wurde. Bei eingerollten Haken, Gewindebolzen, Gewindestopfen oder Schraublaschen tritt keine Biegespannung auf, deshalb bleibt die Sigma-Spalte leer. Außerdem wird in dem Fall unter Ansicht\Goodman\Öse auch kein Goodman-Diagramm mit Biegespannungen angezeigt.

Patentiert-gezogener Federstahldraht ist genormt in der EN 10270-1, Drahtsorten SL, SM, SH, DM, DH. "S" steht für statisch, "D" für dynamisch. Zugfestigkeitsklasse "L" für low, "M" für middle, "H" für high.

Die mechanischen Eigenschaften in ISO 4858-2 sind gleich wie EN 10270-1. Der einzige Unterschied ist, dass es Drahtsorte DM nach ISO 4858-2:2002 schon ab 0,08 mm Drahtdurchmesser gibt, und nach EN 10270-1 erst ab 0,3mm. Und die chinesische GB/T 4357 ist wiederum genau gleich wie ISO 4858-2.

ISO 4858 ist von 2002, eine neuere Ausgabe gibt es nicht.

GB/T 4357 ist von 2009 und identisch mit ISO 4858-2:2002

Die aktuelle EN 10270-1 ist von 2017. Bei den mechanischen Eigenschaften wurde ein Schreibfehler bei der Zugfestigkeit von SM und DM bei d=15mm gegenüber EN 10270-2: 2012 und EN 10270-2:2008 korrigiert. In EN 10270-2:2001 und somit auch in ISO 4858-2 und GB/T 4357 ist dieser Wert aber noch korrekt.

Für die Federprogramme sind nur die Tabellen mit den mechanischen Eigenschaften und Toleranzen relevant, andere Inhalte wie Lieferformen und Lieferbedingungen wurden nicht verglichen.

Der einzige Unterschied beim Vergleich der Tabelle mit mechanischen Eigenschaften der Norm von 2017 mit der von 2001 ist nur, dass die Durchmesserbereiche in der neueren Norm mathematisch korrekt abgegrenzt sind ("14<d<=15", "15<d<=16" statt "d bis 15", "d bis 16"). Die Festigkeitswerte in den Normen von 2001 und 2017 sind genau gleich.

Die Fehlermeldung bedeutet, dass die Relaxation der Feder bei F2 größer ist als die Toleranz der Federkraft F2. Für einen Fall gilt diese Fehlermeldung aber nicht: Wenn für die Federkraft F1 eine Toleranz gesetzt sein soll, für die Federkraft F2 aber nicht, gibt es dafür den Trick, obere und untere Toleranz 0 zu setzen. Die Toleranz ist dann aber nicht 0, sondern frei, die Federkraft F2 wird dann ohne Toleranz ausgegeben. Die Fehlermeldungen "F2,48h<F2min" erscheinen jetzt nur noch, falls für die Federkraft F2 eine "richtige" Toleranz eingegeben wurde.

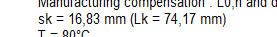
Bei FED6 wird der Knickfederweg sk in den Quick-Ansichten ergänzt.

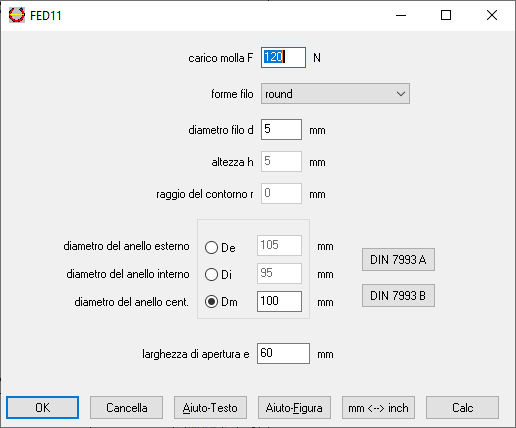
Von FED8, FED11,FED15, FED16 gibt es jetzt auch eine italienische Version. Das Programm ist in italienischer Sprache, Handbuch, Hilfetexte und Hilfebilder sind englisch. Damit gibt es außer FED10 und FED12 alle Federprogramme auch in italienisch

Für Anzahl der Wellen 7.0 – 9.5 war der Faktor K = 2.9 statt 2.3 bei der Berechnung der Federrate nach Smalley verwendet worden. Korrigiert in Version 2.5

Bei Schraubenwellfedern ist wichtig, daß die Wellenberge genau aufeinander liegen, sonst können im Extremfall durch Verdrehung die Wellenberge in die Wellentäler gedrückt werden. Dann sind die gemessenen Federkräfte viel kleiner als die berechneten Werte. Die Kräfte bei Blocklänge stimmen dann wieder überein, weil es dann keine Wellenberge und Wellentäler mehr gibt.

In FED14 wird jetzt auch die Drehfederrate berechnet und mit ausgedruckt. Als "Rtorsion" in Nmm/° und als "Rto/r" in N/° und als "Rto/r²" in N/mm (im mittleren Windungsdurchmesser). Wenn die Drehfederrate klein im Vergleich zur Axial-Federrate ist, dann ist die Gefahr groß, daß sich die Schraubenwellfeder unter Last verdreht und die Wellenberge in die Wellentäler gedrückt werden. In der Quick3-Ansicht wird "R torsion" nur ausgegeben falls mindestens 5 mal kleiner als die Federrate R. Wichtig ist in dem Zusammenhang auch die Federrate "R torsion*n", das ist die Drehfederrate zwischen zwei aufeinanderliegenden Windungen, während "R torsion" bzw. "Rto/r²" die Drehfederrate der gesamten Feder bezogen auf den mittleren Windungsdurchmesser ist.

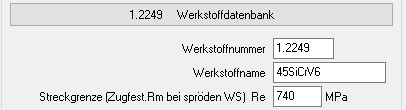
Für spröde Werkstoffe kann man für die Bestimmung der zulässigen Flächenpressung plim die Zugfestigkeit Rm statt der Streckgrenze Re verwenden. Bei Auswahl aus der Werkstoffdatenbank wird jetzt Rm statt Re übernommen., falls Re=0 ist.

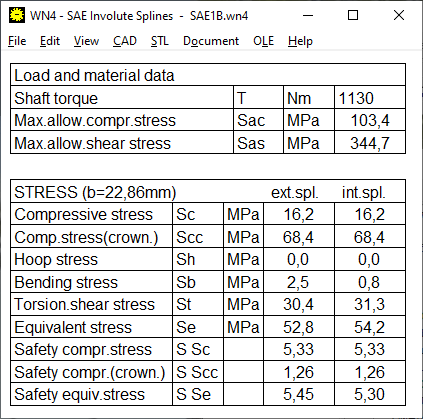
Die Festigkeit von SAE-Zahnwellenverbindungen werden berechnet nach SAE Design Guide for Involute Splines. Bei Überschreiten der zulässigen Spannung werden Fehler gemeldet. Zusätzlich werden jetzt noch Sicherheiten berechnet:

Equivalent stress safety S Se = Sas/Se * 2*Lf / (Ko*Km)

Compressive stress safety S Sc = Sac/Sc * Lw / (Ko*Km)

Dann wird noch die Pressung bei Breitenballigkeit (crowning) berechnet:

Compressive stress (crown.) safety S Scc = Sac/Scc * Lw / (Ko*Km)

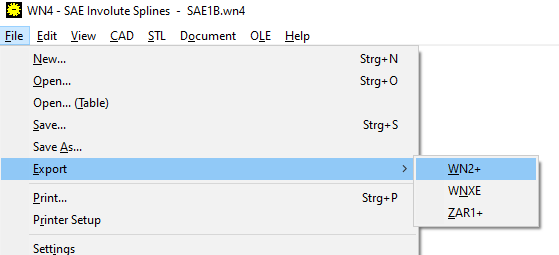
Paßverzahnungen nach SAE und ISO 4156 kann man jetzt exportieren, d.h. speichern im Dateiformat WNX für WNXE, WN2 für WN2+ und ZAR für ZAR1+. Export in WNXE ist sinnvoll, wenn man z.B. zu einer Standard-Zahnnabe eine Zahnwelle mit größerem oder kleinerem Flankenspiel konstruieren will. Eine Anwendung für Export in WN2+ (nur mit Plus-Version möglich) wäre eine Festigkeitsberechnung nach DIN 5480 für eine Paßverzahnung nach ANSI B92.1 oder ISO 4156. Und in ZAR1+ kann man die Abmessungen exportieren um zu schauen, wie eine Zahnwelle im Zahnradprogramm konstruiert wird.

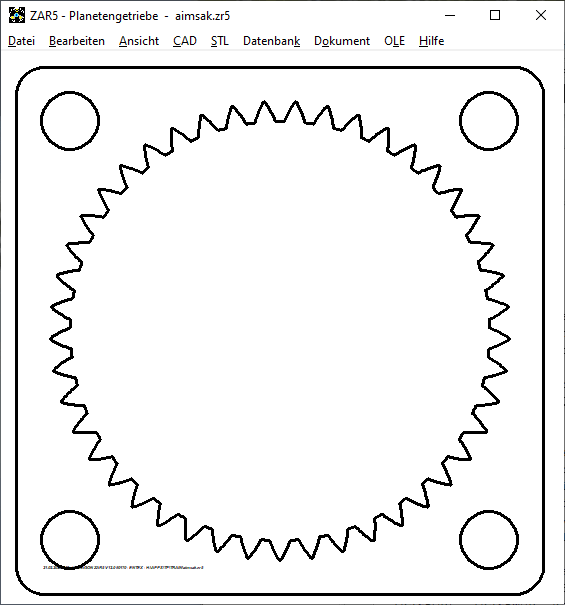
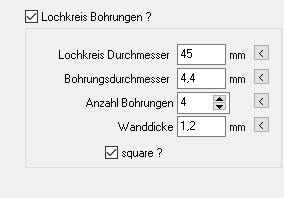
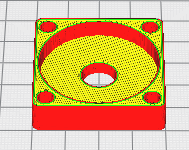
Das Hohlrad von Planetengetrieben kann man jetzt auch mit quadratischer Außenkontur drucken. Der Kranzdurchmesser dB ist dann die Kantenlänge a. Wie bei rundem Außendurchmesser kann man auch hier Befestigungsbohrungen auf einem Lochkreis festlegen. Die Anzahl der Bohrungen ist sinnvollerweise immer 4, der Lochkreisdurchmesser kann größer und dB kleiner sein als bei zylindrischem Hohlrad.

Unter "STL" im Menü kann man jetzt auch Gehäuse für Planetengetriebe drucken mit dem 3D-Drucker. Die Außenkontur kann rund oder quadratisch sein.

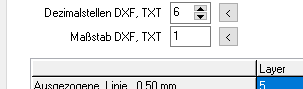
Bei den CAD Einstellungen gibt es eine neue Option zum vergrößern oder verkleinern von Zeichnungen als DXF- oder TXT-Datei. Wenn man z.B. die DXF-Datei in inches ausgeben will, kann man einen Maßstab 1/25.4 = 0.03937 konfigurieren.

Bedauerlicherweise wird Windows 7 von Microsoft nicht mehr unterstützt, so dass die meisten Anwender gezwungenermaßen auf Windows 10 umstellen werden. Weil Windws 10 Updates manchmal Partitionen auf der Festplatte verändern (meistens ist die Festplatte danach um 0.5 MB "geschrumpft"), sollten Sie HEXAGON Software nicht auf der Windows-Partition C: installieren, sondern auf einer anderen Partition oder Laufwerk, falls vorhanden. Sie können HEXAGON Software sogar auf einer externen Festplatte installieren, dann kann man bei einem späteren Umzug auf einen anderen PC die Software einfach mitnehmen. Bei Änderung von Seriennummer oder Festplattendaten durch Win10-Updates brauchen Sie sonst jedesmal neue key codes.

Vor 20 Jahren war Berlin ein Paradies für Fahrradtouristen. Zum Radfahren war auf den Gehwegen eine rote Radspur eingerichtet, auf dem Fahrrad konnte man gefahrlos die Stadt erkunden. Vermutlich zum Schutz der Fußgänger wurden die Radspuren auf die Strasse verlegt, mit unübersehbaren Folgen in der Unfallstatistik der getöteten Radfahrer. Noch gefährlicher ist es, wenn die Radspur neben parkenden Autos entlang führt. Bei unachtsam geöffneten Autotüren hat der Radfahrer keine Chance, weil von hinten nicht erkennbar ist ob in einem parkenden Fahrzeug jemand sitzt oder nicht. Vielleicht wäre ein Sensor im Außenspiegel eine Lösung, welcher bei Gefahr eine Art Kindersicherung an der Fahrertür einschaltet und das unachtsame Öffnen der Tür verhindert.

Weil Lkw, Kleinbusse und SUV beim Rechtsabbiegen geradeaus fahrende Radfahrer übersehen, werden komplizierte Rechtsabbiegeassistenten mit Kamera und Monitor für Lkw empfohlen. Dabei ginge das viel einfacher mit einer intelligenten Ampel für Rechtsabbieger, welche erst auf grün schaltet, wenn geradeaus fahrende Radfahrer den Kollisionsbereich verlassen haben. Verglichen mit der Sensorik für ein selbstfahrendes Auto wäre der Aufwand für eine Ampel mit intelligentem rotem Pfeil ein Klacks. In dem Zusammenhang könnten auch gleich Sensoren für intelligente Ampel- und Verkehrsflußsteuerungen eingebaut werden. Ampeln optimal zu programmieren ist nicht einfach. Trotzdem ist es ärgerlich, wenn an einer Ampelkreuzung alle warten und keiner fährt. Schlecht programmierte Ampeln kosten die Verkrehrsteilnehmer viel Zeit und Geld, 24 Stunden am Tag, jahrelang.