 | Deutsch
| English
| Deutsch
| English
FED2+: Ösendarstellung bei Einlegeteilen

Bei eingerollten oder eingeschraubten Haken oder Schrauben wird keine Öse mehr gezeichnet, stattdessen wird der beschreibende Text ausgedruckt sowie eine Linie bei LK und LH.
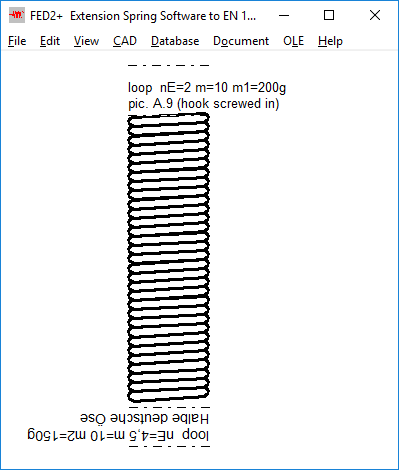
FED2+: Gewicht von Einlegeteilen
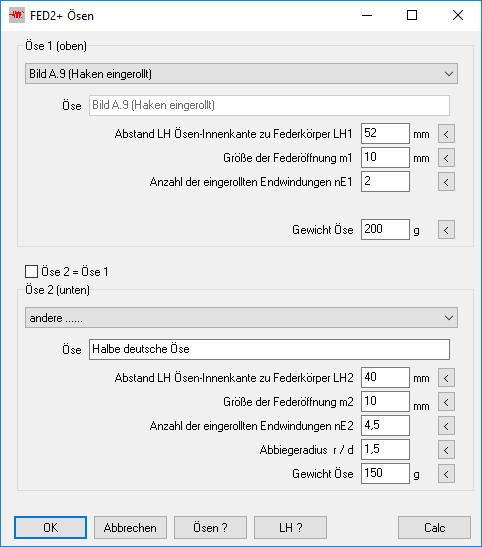
Bei eingerollten oder eingeschraubten Haken oder Schrauben kann man jetzt das Gewicht der Einlegeteile bzw. der Öse eingeben, diese werden dann zum Gewicht der Zugfeder addiert.
FED2+: Abbiegeradius Ösen
Den Abbiegeradius kann man jetzt für Öse 1 und Öse 2 getrennt eingeben. An der Berechnung der Biegespannung ändert sich dadurch nichts, entscheidend ist der kleinere der beiden Werte.
FED2+: Ösenstellung bei Gewindebolzen
Bei eingeschraubten Gewindebolzen oder bei Zugfedersträngen ohne Ösen wird die Ösenstellung in der Quick3-Ansicht nicht mehr angezeigt.
FED6, FED7: Nummerierung Windungsabschnitte
Weil die Feder vertikal am Bildschirm angezeigt wird, werden die Enden "oben" und "unten" benannt. Bei der Eingabe der Windungsabschnitte beginnt man "unten", Abschnitt 1 ist bei der vertikal dargestellten Feder der unterste Abschnitt. Bei den Endwindungen ist E1 die untere Endwindung und E2 die obere Endwindung. Die Tabelle mit dem Windungen begann mit 1 (oben) und endete mit der letzten Windung (unten). Weil dies umgekehrt ist wie bei der dargestellten Federzeichnung, wird die Tabelle jetzt umgekehrt dargestellt: zuerst obere Endwindung E2, dann beginnend mit der letzten Windung bis zur ersten Windung und Endwindung E1. Bei der Fertigungszeichnung ändert sich nichts, dort wird die Tabelle "liegend" dargestellt.
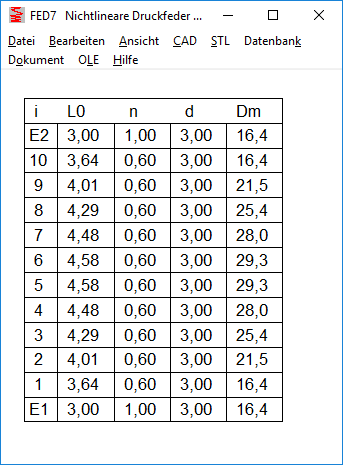
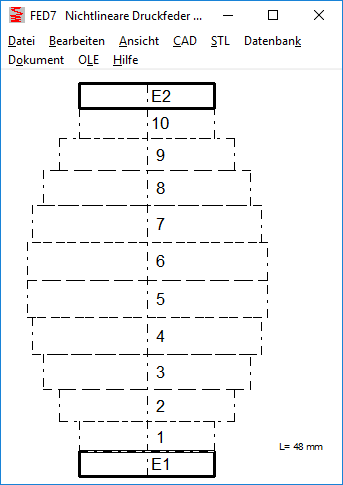
FED7: In Reihe geschaltete Druckfedern berechnen
FED7 kann man auch verwenden, um in Reihe geschaltete Druckfedern zu berechnen. Für die Berechnung der Blocklänge kann man die Druckfedern in 2 oder 3 Abschnitten eingeben: Endwindungen unten/oben und federnde Windungen. Endwindungen mit L0i=nE*d, allerdings kann man nicht unterscheiden zwischen angelegten und geschliffenen Windungen, deshalb ist die FED7-Berechnung hier nicht ganz genau.
Parallel geschaltete Druckfedern berechnen
Bei parallel geschaltetetn Druckfedern beginnt die Federung mit L0 der längsten Feder und geht auf Block wenn die erste Feder aufsetzt.
Es wurde angefragt, für parallel geschaltete Federn eine neue Software zu machen. Falls größerer Bedarf besteht, machen wir das.
ZAR1+: Exzentergetriebe mit ZAR1+ konstruieren
Im Infobrief 167 vor einem Jahr wurde gezeigt, wie man mit ZAR1+ die Zahnradpaarung für Exzenter-Abwälzgetriebe aus außen- und innenverzahntem Zahnrad berechnen kann. Hierzu gab es Nachfragen, deshalb hier die Vorgehensweise mit ZAR1+. In dem Beispiel aus Info 167 war die Zähnezahldifferenz 2 Zähne, zur Erreichung einer großen Übersetzung soll das Abwälzrad aber nur um 1 Zahn kleiner sein als das Hohlrad.
Beim Exzenter-Abwälzgetriebe ist meist das Hohlrad fest, das Wälzrad wird angetrieben mit einer Exzenterwelle. Exzentrizität ist der berechnete Achsabstand. Abtriebsseitig wird die Drehung des Wälzrads um das Zentrum aufgenommen, das geschieht hier durch eine Scheibe mit Bolzen und Rollen auf einem Lochkreis, die in Bohrungen im Wälzrad eintauchen. Bohrungsdurchmesser der Wälzradbohrungen ist der Rollendurchmesser + 2*Exzentrizität. Ein Exzentergetriebe mit einem Zahnradpaar mit Evolventenverzahnung ist eine günstige Alternative zu ähnlichen Getriebekonzepten mit Zykloidgetriebe, Wellgetriebe, Cyclo Drive, Harmonic Drive, Galaxiegetriebe usw.
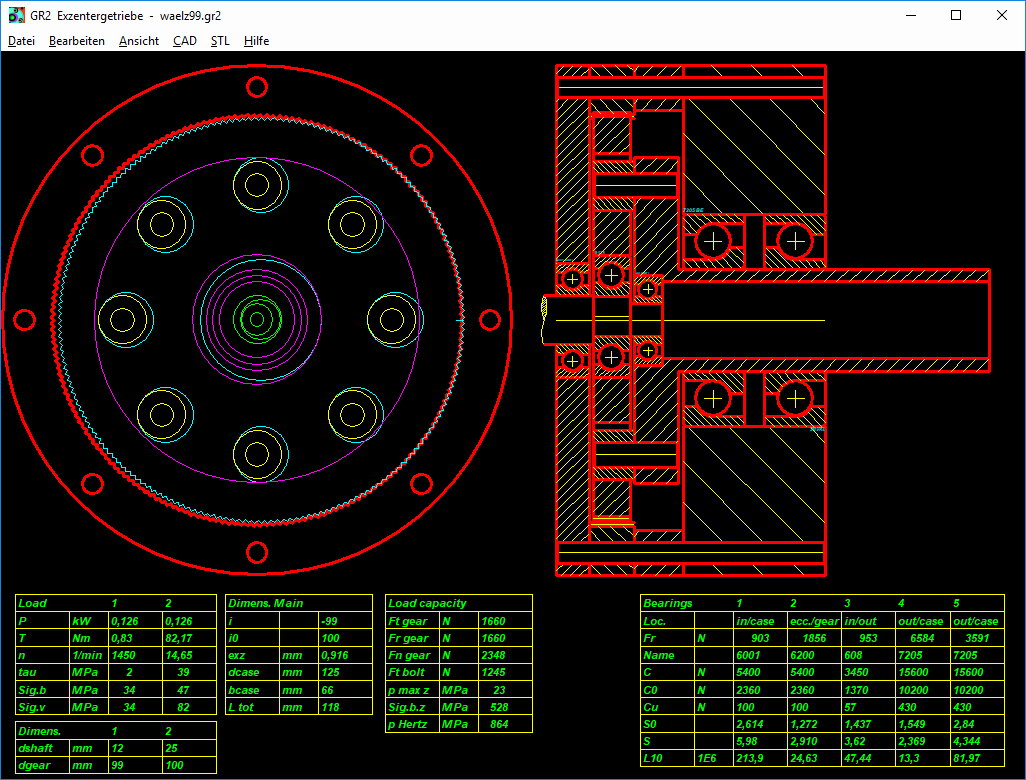
Ein Exzenter-Abwälzgetriebe ist sinnvoll, wenn man mit nur einer Stufe eine hohe Übersetzung realisieren will. Die größtmögliche Übersetzung erreicht man, wenn die Zähnezahldifferenz möglichst klein ist, also 1 Zahn. Bei einer Zähnezahl Wälzrad 30 Zähne und Hohlrad 31 Zähne ist das Übersetzungsverhältnis –30, die Drehrichtung von Antriebs- und Abtriebswelle ist entgegengesetzt. Wenn man den Bolzenteller blockiert und am Hohlrad abtreibt, ist die Übersetzung sogar noch etwas größer (+31), und die Drehrichtung gleich wie bei der exzentrische Antriebswelle. Wenn man die Exzenterwelle festhält, laufen Hohlrad und Bolzenteller in gleiche Richtung, die Drehzahl unterscheidet sich um das Übersetzungsverhältnis 31/30=1.0333. Wenn beispielsweise der Bolzenteller (Carrier) mit 1000/min umläuft, dreht das Hohlrad mit 967.7/min.
GR2 wird ein neues Berechnungsprogramm für Exzentergetriebe. GR2 berechnet Antriebswelle mit Exzenter, Abtriebswelle mit Bolzenteller und alle 5 Wälzlager. Nicht jedoch die Zahnräder, das kann man mit ZAR1+. Oder man verwendet Zykloiden, Wellgetriebe, oder gar Reibradgetriebe.
Mit ZAR1+ werden die Zahnräder ausgelegt. Zähnezahl Wälzrad 30 Zähne, Hohlrad 31 Zähne.
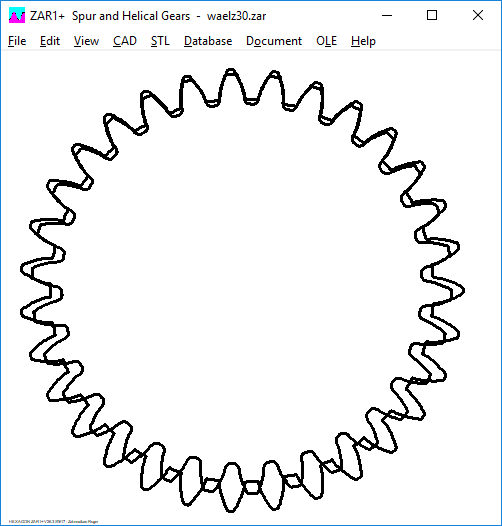
Der erste Versuch mit z1=30, z2=-31, alpha=20°, x=0, Zahnhöhe (1+1,25)*mn. So geht das natürlich nicht.
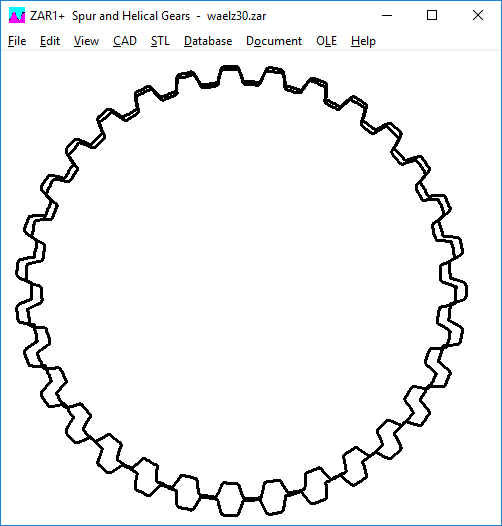
Zweiter Versuch mit halbierten Zahnhöhenfaktoren (Zahnhöhe (0.6+0.5)*mn).
Nun wird der Eingriffswinkel geändert von 20° in 45°.
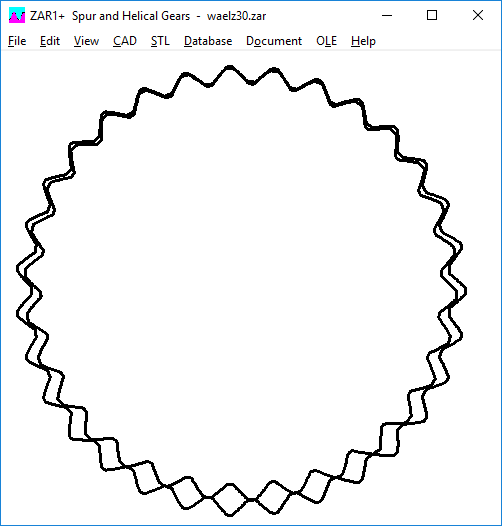
Dritter Versuch mit Eingriffswinkel alpha 45° statt 20°. Immer noch Eingriffsstörungen.

Vierter Versuch mit Profilverschiebung x2= -0.5. Negative Profilverschiebung vergrößert das Hohlrad oder verkleinert das Wälzrad, hier mit x2=-0,5, x1=0. Die Eingriffsstörungen sind weg. Der berechnete Wälzkreis liegt jedoch weit außerhalb der Verzahnung, der berechnete Wälzkreisdurchmesser ist fast doppelt so groß wie der Teilkreisdurchmesser. Aber die Animation zeigt, daß die Verzahnung für diese Anwendung einsetzbar ist.
Es gibt keinen Linienkontakt auf der Eingriffsgeraden, dafür 2 Kontakte links und rechts der Eingriffslinie, 2 bis 3 Zähne entfernt. Negativ bezüglich Reibung und Gleiten, aber positiv bezüglich Tragfähigkeit sowie Verdrehflankenspiel und Selbsthemmung. Die Fehlermeldung in ZAR1+ wegen Waelzkreis, Eingriffsgerade und epsilon alpha < 1 muss man halt ignorieren.

Man kann aber auch die Profilverschiebung zurück auf 0 setzen, und dafür die Zahnhöhenfaktoren weiter reduzieren auf (0,5+0.4)*mn, damit kommt man auch zum Ziel.

Obwohl Übersetzungsverhältnis, Modul und Teilkreisdurchmesser für beide Varianten gleich sind (i=30, mn=1mm), unterscheidet sich die Exzentrizität der Exzenterwelle: ohne Profilverschiebung a=0,5 mm, aber mit Profilverschiebung a=0,916 mm, fast doppelt so groß. Beim profilverschobenen Hohlrad sind Kopf- und Fußkreisdurchmesser größer als der Teilkreisdurchmesser.
Für die Herstellung von Modellgetrieben mit 3D-Drucker kann man in ZAR1+ unter "STL\Rad1,2" einen Lochkreis mit Bohrungen eingeben:
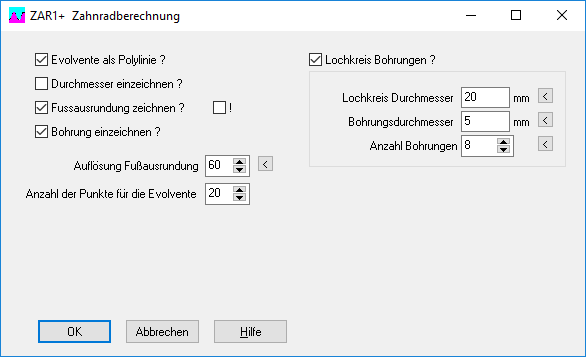
Für das Hohlrad die Bohrungen für Befestigungsschrauben und/oder Stifte, und für das Wälzrad die Bohrungen für die Rollen der Abtriebswelle. Beim Hohlrad ist der eingegebene Bohrungsdurchmesser der äußere Zahnkranzdurchmesser.

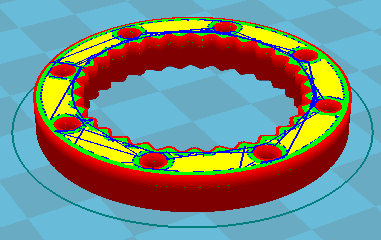
Wenn Hohlrad und Wälzrad fertig sind, kann man mit GR2 Antriebswelle, Abtriebswelle und Lagerdeckel als STL-Datei generien und mit 3D-Drucker herstellen.


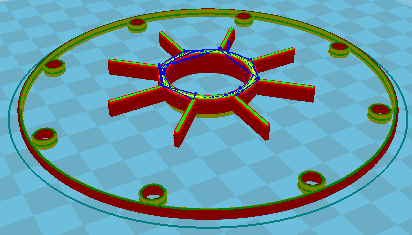
Die Modellgetriebe aus dem 3D-Drucker mit Übersetzungsverhältnis 1:10, 1:30 und 1:100 funktionieren prima, nur etwas laut bei hoher Antriebsdrehzahl.

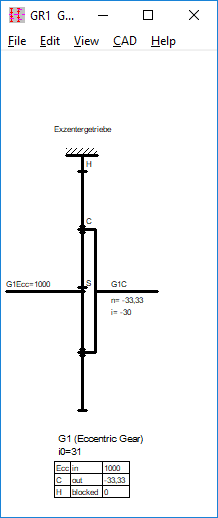
GR1: Ergänzt um Exzentergetriebe
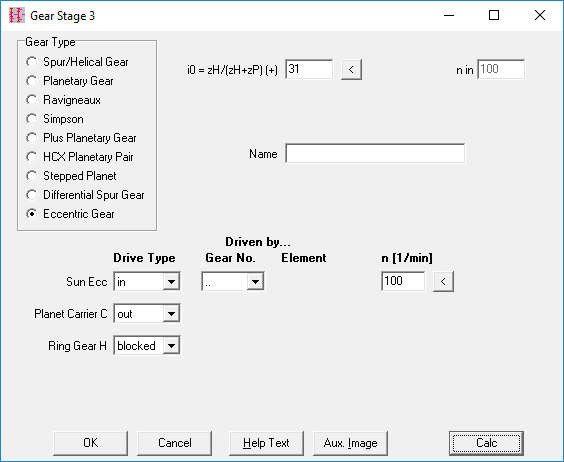
In die Getriebebaukasten-Software GR1 wurden Exzentergetriebe aufgenommen. Die Relativgeschwindigkeiten kann man ähnlich berechnen wie bei einem Planetengetriebe. Das Wälzrad ist das Planetenrad, die Exzenterwelle das Sonnenrad, der Bolzenteller ist der Steg, das Hohlrad gleich wie beim Planetengetriebe. Die virtuelle Zähnezahl des Sonnenrads ist die negative Zähnezahldifferenz: zS = zH + zP. Das Übersetzungsverhältnis bei blockiertem Steg ist i0 = zH/zS = zH/(zH+zP). Die Standübersetzung i0 ist positiv, wie bei einem Plus-Planetengetriebe.
GEO5 Demoversion
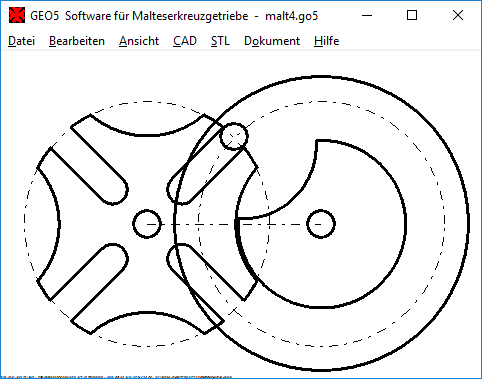
Von GEO5 (Malteserkreuztrieb) gibt es jetzt auch eine Demoversion.
Alle Programme: Init-Datei automatisch laden
Mit einer NULL-Datei kann man werkskonforme Standardeinstellungen, z.B. Werkstoff und Toleranzklassen der Maschinenlemente automatisch laden. Allerdings wird die NULL-Datei aus dem konfigurierten Ordner geladen, und dieser kann bei Netzwerkversionen mit vielen Anwendern bei jedem User anders sein. Wenn jeder Anwender mit denselben Anfangsdaten seine Berechnung starten soll, kann man jetzt im Programmordner eine Berechnungsdatei mit dem Dateinamen "INIT" speichern (z.B. "init.fed" neben "wfed1.exe"), dann wird diese INIT-Datei bei Programmstart automatisch geladen. Falls es sowohl NULL-Datei im Datenverzeichnis als auch INIT-Datei im Programm-Verzeichnis gibt, hat die INIT-Datei Priorität.
Die Dichte von Luft bei 0°C ist 1,293 kg/m³, die Dichte von NO2 ist ca. 3,6 kg/m³. Demnach ist es wahrscheinlich, dass die Stickoxid-Wolken nach Abkühlung und bei Windstille am Boden wabern. Folglich müssten Messungen in Erdnähe höhere Stickoxidkonzentrationen ergeben. Interessant wären vergleichende Messungen in verschiedenen Messhöhen. Auch interessant wäre ein Vergleich entlang derselben Straße mit genau demselben Verkehrsaufkommen, einmal entlang einer Häuserschlucht, und dann noch an einer Stelle ohne unmittelbare Bebauung. Weitere Parameter wären Windgeschwindigkeit, Temperatur, Luftdruck. Leider gibt es NOx-Meßgeräte nicht im Handel, sonst könnte man selber messen.
Wenn sich das Stickoxidgas am Boden sammelt, ist die richtige Meßhöhe die Größe eines Kleinkindes, das schon laufen kann. Quasi ein Kind auf Augenhöhe mit dem NOx-Sensor. Anders ist es bei Kohlenmonoxid. Die Dichte von CO ist 1,25 kg/m³, also etwas leichter als Luft. Kohlenmonoxid entweicht nach oben. Gefährlich wird es in geschlossenen Räumen mit niedriger Decke. Den Jugendlichen, welche eine Hütte für eine Feier mit einem Notstromaggregat beleuchtet und beschallt haben, wurde das zum tödlichen Verhängnis. Bei Stickoxid und Feinstaub dauert es länger. Asthma ist zur häufigsten chronischen Erkrankung im Kindes- und Jugendalter geworden.