Nachweis der Abstreifsicherheit axial beanspruchter Einschraubverbindungen.

Nachweis der Abstreifsicherheit axial
beanspruchter Einschraubverbindungen.

von

Dipl.-Ing. Gerh. Friedr. Dose
Prof. Dr.-Ing. Wilhelm Schwarz

G. F. Dose
Goethestraße 47
D 69514 Laudenbach

Prof. Dr.-Ing. Wilhelm Schwarz
Universität Siegen
Fachbereich 11 Maschinentechnik
Konstruktion- und Fördertechnik
Postfach 101240
D 57068 Siegen

Inhaltsverzeichnis

Seite
1 Allgemeines 3

2 Abstreifsicherheit 3

3 Scherspannungsfaktor 4

4 Geometrische Herleitung 5

5 Einschraubtiefe 6

6 Sicherheitsnachweis für die Gewindegänge 7

7 Berücksichtigung der Toleranzen 7

8 Abstreifversuche 7

9 Schrittweise Berechnung 7

9.1 Berechnung der Einschraubtiefe 7

9.2 Berechnung des Scherspannungsfaktors 8

10 Literatur 8

Nachweis der Abstreifsicherheit axial beanspruchter
Einschraubverbindungen.

1 Allgemeines

Für die Bestimmungsgrößen der verschiedenen Gewindearten, wie Spitz-, Trapez-, Rund- und Sägengewinde, wird die DIN 2244 herangezogen. Damit gilt mit Ausnahme des Sägengewindes nach DIN 513 T. 1 ... 3 für alle Gewindearten, daß die Höhen der Grunddreiecke H nach folgender Gleichung berechnet werden:

H = ½ * P * ctg (a /2) (1)

mit P = Steigung (Ganghöhe)
und a = Flankenwinkel.

errechnet werden.

Bild 1: Nullprofil eines Spitzgewindes

2 Abstreifsicherheit

Im Zuge der Konstruktionen von Einschraubverbindungen, wie bei Gewindelast- und Zurrblöcken, Ringschrauben, Kugeldrehverbindungen o. ä. sind neben den Bauteilbemessungen auch Festigkeitsnachweise zu erbringen, um sicherzustellen, daß die Schraubverbindung haltbar ist. Über die Berechnung solcher Schraubverbindungen mit metrischen ISO-Gewinden nach DIN 13/14 existieren diverse Beiträge im Schrifttum.

Die Berechnung soll so angelegt sein, daß eine hinreichende Einschraubtiefe zu ermitteln ist, wobei im allgemeinen davon ausgegangen wird, daß die Werkstoffestigkeit des Körpers mit dem Mutterngewinde (Mutter) gleich dem der Schraube (Bolzen) ist. Bei unterschiedlichen Werkstoffestigkeiten von Mutter- und Bolzen wird auch bei den bisher anerkannten Berechnungsverfahren nach der VDI-Richtlinie 2230 [1] angenommen, daß die Gewindegänge je nach Werkstoffpaarung entweder in der Nähe des Grund des Muttergewindes bei d oder des Bolzengewindes bei D₁ abgestreift werden. [2]

Anhand von vielen Versuchen mit unterschiedlichen Werkstoffpaarungen [3, 4, 5] wurde jedoch festgestellt, daß die vorstehenden Annahmen im allgemeinen nicht zutreffend sind, sondern daß Bolzen- und Mutterngewinde gleichzeitig versagen können. Dabei ergibt sich ein glatter Abscherzylinder mit der Länge der Einschraubtiefe m und dem Abstreifdurchmesser dt . Letzterer liegt im allgemeinen zwischen den vorgenannten Durchmessern d und D₁, also D₁ £ dt £ d.

Die Abweichung des Abstreifdurchmesser vom theoretischen Flankendurchmesser des Gewindes D₂, bzw. d₂ hängt von der Werkstoffpaarung ab. Die nach der Richtlinie VDI 2230 [1] berechneten Einschraubtiefen können dagegen zu größeren Ungenauigkeiten und Risiken führen. [3]

Bei Festigkeitsnachweisen für Anwendungen mit hohen Gefahrenpotential, sind definierte Sicherheitsnachweise zu führen, hierzu wird die statische Sicherheit n als das Verhältnis der Abscherfestigkeit t _m zur vorhandenen Abscherbeanspruchung am Abscherzylinder t definiert.

n = t _m / t (2)

Obwohl sich der Durchmesser des Abscherzylinders im allgemeinen so einstellt, daß das Versagen von Mutter- und Bolzengewinde gleichzeitig erfolgt, wird der Sicherheitsnachweis für jedes der beiden Teile gefordert. Ferner ist der Nachweis der statischen Bruchsicherheit des Bolzen erforderlich.

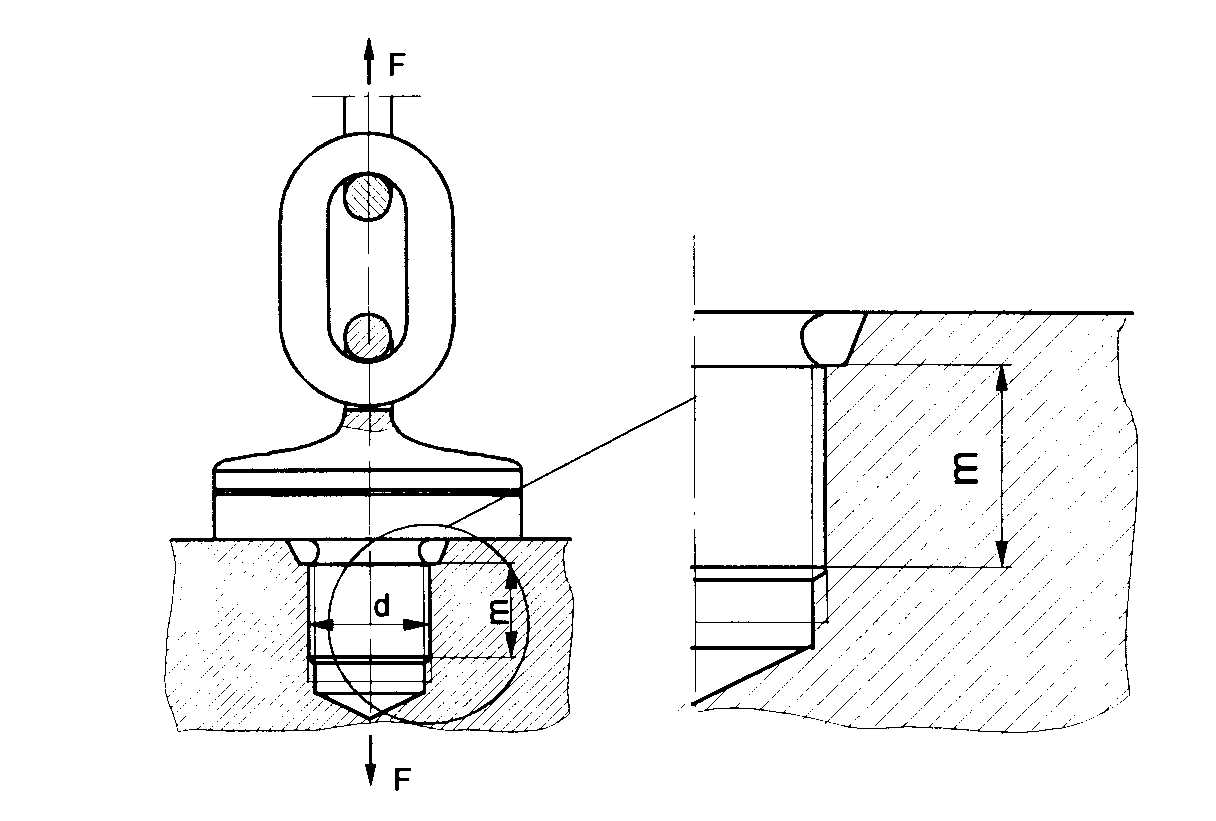
Vorausgesetzt, daß das Gewinde beim Einschrauben nicht überbeansprucht wird und die Belastungsrichtung in axialer Richtung auf Zug erfolgt, liegt eine Abscherbeanspruchung vor (Bild 2).

Bild 2: Wälzgelagerter Wirbelblock mit Einschraubverbindung

Die Abscherfestigkeit t _m läßt sich für gängige Stähle nach der Hypothese der Gestaltsänderung nach von Mises aus der Zugfestigkeit R_m berechnen:

t _m » R_m /Ö 3 (2a)

Dieser Zusammenhang wird hier in allgemeiner Form formuliert, indem ein Scherspannungsfaktor b eingeführt wird, der gewindespezifische Einflüsse auf den Abschervorgang enthält und formal für alle interessierenden Werkstoffe gilt:

t _m = b * R_m (3)

Diese Darstellung gilt für Muttern (Index M) und Bolzen (Index B) gleichermaßen, also

t _m,M = b _M * R_m,M (3a)

und

t _m,B = b _B * R_m,B (3b)

3 Scherspannungsfaktor

in mehr als 100 Versuchen mit unterschiedlichsten Werkstoffen für Bolzen und Muttern wurde nachgewiesen, daß die Gestaltsänderungshypothese nur bei bestimmten Werkstoffen (ferritisch und martensitische Stähle) in guter Näherung zutrifft [3].

Für alle genannten Versuche wurden serienmäßig hergestellte Schraubenbolzen M 20 bzw. M 16, jeweils aus derselben Vergütungscharge, mit dem Abmaß von 6g eingesetzt, und die Muttern wurden aus den verschiedenen Werkstoffen mit einem Abmaß von 7H gefertigt. Mit Ausnahme des austenitischen Bolzens waren alle Bolzengewinde gerollt. Sofern der Scherspannungsfaktor aus Versuchsergebnissen abgeleitet wird, enthält er neben den Werkstoffeigenschaften, etwaige Biegespannungseinflüssen sowie das Spiel aus den Toleranzen, Kerbeinflüsse und Stützwirkungen im Gewindeteil. Im folgenden werden die theoretischen Grundlagen für die Ermittlung der Scherspannungsfaktoren aus Versuchsergebnissen hergeleitet. Vorausgesetzt wird hierfür, daß die tatsächlichen Zugfestigkeiten der Proben bekannt sind.

Gemessen wird die Zugkraft F der Schraubenverbindung, bei der das Gewinde abgestreift wird. Der gesamte Abstreifzylinder hat die Gesamtabscherfläche At :

At = m * dt * p (4)

wobei m die gesamte wirksame Einschraubtiefe bedeutet. Ebenso wird der Abstreifdurchmesser dt gemessen. Im allgemeinen besteht die Abscher-/Abstreiffläche aus Mutter- und Bolzenanteil, die nur gleichzeitig abscheren können. Wegen des actio/reactio-Prinzips ist die Versagenskraft F für den Bolzengewindeanteil a _B und Mutterngewindeanteil a _M gleich groß. Für die Abscherflächenanteile gilt:

At _B = a _B * m * dt * p (4a)

_{At
_M = a
_M * m * dt
* p
(4b)
Mit der Abscherspannung beim Versagen für das Muttergewinde:
t
_mM = F / (a
_M * m * dt
* p
) = b
_M * R_mM (5)
läßt sich der Scherspannungsfaktor für die Mutter berechnen:
b
_M = F / (R_mM * a
_M * m * dt
* p
) (5a)
Analog hierzu gilt für den Bolzen:
b
_B = F / (R_mB * a
_B * m * dt
* p
) (5b)

4 Geometrische Herleitungen
Die Abscherfläche besteht aus parallel-gewendelten Streifen abgescherter Mutter- und Bolzengewindegänge. Der Abscherzylinder At
mit dem Abstreifdurchmesser dt
und der Abstreiflänge m enthält die beiden Abscherflächen von Bolzen und Mutter.
At
= At
_B + At
_M (6)
Die anteile der abscherflächen eines Gewindeganges hängen vom Abstreifradius rt
ab. Mit h_M für das Muttergewinde und h_B für den Bolzen gilt gemäß Bild 3:
P = h_B + h_M (7)

Bild 3: Breiten h der Abscherflächen.
Die Teilhöhen h_M und h_B auf einen Gang des Abscherzylinders lassen sich anhand von Bild 3 berechnen:
h_B = P/2 – 2*D
ht
(8a)
und h_M = P/2 + 2*D
ht
(8b)
mit D
ht
= (rt
– r₂)*tan (a
/2) (9)
worin r₂ = Flankenradius des Gewindes bedeutet.
Die Verhältnisse der Teilhöhen zur Steigung P ist gleich dem Scherflächenanteilsfaktor a
, also für den Bolzen
a
_B = h_B /P (10a)
und für die Mutter
a
_M = h_M /P (10b)
Der Anteil für das Bolzengewinde ergibt sich nach Bild 3 mit Gl. (8a) zu:
a
_B = ½ – (dt
– d₂) * tan (a
/2) / P (11a)
und für das Mutterngewinde ergibt sich nach Gl. (7)
a
_M = ½ + (dt
– d₂) * tan (a
/2) / P (11b)
Die Abscherflächen-Anteilsfaktoren ergänzen einander zum Endwert 1,0. Daher gilt für den Bolzen
a
_B = 1 – a
_M = At
_B / At
(12a)
und für die Mutter
a
_M = 1 – a
_B = At
_M / At
(12b)
Anhand dieser Anteilsfaktoren können die Abscherflächen von Bolzen und Mutter angegeben werden:
At
_B = At
*a
_B (13a)
und At
_M = At
*a
_M (13b)
Weil Bolzen- und Mutterngewinde immer gleichzeitig, also bei gleicher Belastung, versagen, gilt:
Ft
_m = At
* a
_B * t
_mB = At
* a
_M * t
_mM = At
*(1 – a
_B) * t
_mM (14)
Die Auflösung nach a
_B ergibt folgende Form, die nur noch von den Scherfestigkeiten der Werkstoffe beider Teile abhängt und deswegen Werkstoff-Faktor genannt wird:
a
_B = t
_mM / (t
_mM + t
_mB) (15a)
a
_M = t
_mB / (t
_mM + t
_mB) = 1 – a
_B (15b)
Nach Gleichsetzung von Gl. (15a) und (11a) ergibt sich der gemeinsame Abstreifdurchmesser zu:
dt
= d₂ + [0,5 – t
_mM / (t
_mM + t
_mB)] * P / tan (a
°/2) (16)

5 Einschraubtiefe
Für den Nachweis, daß das Gewinde mindestens genauso haltbar ist wie der Bolzen, wird die Mindesteinschraubtiefe des Gewindes so festgelegt, daß die Kraft bei Abstreifen des Gewindes der Bruchkraft F_m des Bolzens entspricht. Letztere beträgt unter Berücksichtigung des Spannungsquerschnittes A_S des Bolzens
F_mB = R_m,B * A_s (17a)
mit A_s = ½ (d₂+d₃)²*p
/4 (17b)
Nach Gleichsetzen dieser Bolzenbruchkraft mit der Abstreifkraft des Gewindes nach Gl. (14) beispielsweise für das Bolzengewinde, läßt sich die Mindesteinschraubtiefe berechnen:
m_min ³
(R_mB * A_S) / (p
*dt
*a
_B*t
_mB) (18)
Mit t
_mB nach Gl. (3b) und a
_B nach Gl. (11 a), sowie dt
nach Gl. (16) geht Gl. (18) schließlich in nachstehende Schreibweise über:
m_min = 1/(b
_B*p
)*(t
_mM+t
_mB)/t
_mM*A_S/[d₂+{0,5–t
_mM/(t
_mM+t
_mB)}*P/tan (a
/2)] (19a)
Bei Einsetzen der Zwischenergebnisse lautet die Gleichung dann:

m_min = 1/(b
_B*p
) * 1 / a
_B * A_S / dt
(19b)
6 Sicherheitsnachweis für die Gewindegängen
Die Ist-Werte der Scherspannungen im Bolzengewinde ergeben sich nach der Definition der Abscherspannung mit der Belastung F zu:
t
_B = F_max / (At
* a
_B) (20a)
Die Scherspannung im Muttergewinde ist analog formuliert:
t
_M = F_max / (At
* a
_M) (20b)
Die Sicherheitsnachweise werden sowohl für das Bolzen- als auch für das Muttergewinde geführt:
n
_B = t
_mB / t
_B = b
_B* R_mB / t
_B ³
n
_erf für das Bolzengewinde (21a)
und n
_M = t
_mM / t
_M = b
_M* R_mM / t
_M ³
n
_erf für das Muttergewinde (21b)

7 Berücksichtigung der Toleranzen
Sofern die Gewinde nicht in den üblichen Toleranzen 7H / 6g gefertigt werden, ist zu beachten, daß die Einschraubtiefe um den Betrag vergrößert wird, der sich aus den Toleranzmaßen ergibt. erfahrungsgemäß sind die Abweichungen bei kleinerem Gewindedurchmesser gering, so daß eine rechnerische Vergrößerung der Einschraublänge um ca. 5 % genügt. Bei einem exakten rechnerischen Nachweis sind jedoch die entsprechenden Toleranztabellen der Normen zu berücksichtigen.

8 Abstreifversuche
Umfangreiche Abstreifversuche wurden, wie in [3, 4, 5] aufgeführt, in Zusammenarbeit mit der Qualitätsstelle der Firma Schraubenwerke Fuchs, GmbH, Siegen, durchgeführt. Untersucht wurden Verbindungen mit Schraubenbolzen und Muttern unterschiedlichster Materialpaarungen mit Schrauben mit Gewinde M 20 und M 16 in den verschiedenen Festigkeitsklassen und in austenitischer Qualität. Die realen Zugfestigkeiten aller Proben sind durch begleitende Zugversuche bzw. durch 3.1 B-Zeugnisse nachgewiesen worden. Die Prüfkraft wurde bis zum Versagen der Verbindungen gesteigert. Gemessen wurden Bruchkraft, Einschraubtiefe und Abstreifdurchmesser. Anhand der ober hergeleiteten Gleichungen lassen sich die Scherspannungsfaktoren und die Abstreifdurchmesser berechnen und den gemessenen Werten gegenüberstellen.
Die Gegenüberstellung der berechneten und gemessenen Werte können in [3, 4, 5] eingesehen werden.

9 Schrittweise Berechnung
9.1 Berechnung der Einschraubtiefe
Bei einer schrittweisen Berechnung der Einschraubtiefe, also mit Ermittlung der Zwischenwerte, können folgende Gleichungen angewendet werden:
Zulässige Scherspannung vom Bolzen t
_m,B, = b
_B, * R_m,B (3b)

Zulässige Scherspannung der Mutter: t
_m,M = b
_M * R_m,M (3a)

Werkstoffaktor des Bolzens: a
_B = t
_mM / (t
_mM + t
_mB) (15a)

Werkstoffaktor der Mutter a
_M = 1 – a
_B (15b)

Abstreifdurchmesser: dt
= d₂ + (0,5 – a
_B) * P / tan (a
°/2) (16)

Kraft an der Bruchgrenze: F_m,,B = A_S * R_m,B (17a)

Fläche des Abstreifzylinders At
= F_m,B *(1/t
_mM + 1/t
_mB)

Einschraubtiefe: m_{min, erf} = At
/ (dt
* p
)
Die beiden letzten Gleichungen lassen sich aus der Gleichung (14) in Verbindung mit den Gleichungen (13a) und (13b) herleiten.

9.2 Berechnung des Scherspannungsfaktors
Mit den bekannten Werkstoffwerten des Bolzens. den Werkstoffkennwerten der Mutter und den bei Versuchen festgestellten Daten für die Abstreifkraft bzw. Bruchkraft des Bolzens, den gemessenen Abstreifdurchmesser und die Einschraubtiefe sind folgende Berechnungsschritte erforderlich:
Abscherfläche At
= m * dt
* p
(4)

Scherspannung der Mutter t
_mM = (At
/ F – 1 / t
_mB)^–1

Scherspannungsfaktor der Mutter b
_M = t
_mM / R_m,M}

Die beiden letzten Gleichungen lassen sich aus den beiden vorstehenden Gleichungen im Abschnitt 9.1 ableiten.

10 Literatur:

[1] VDI 2230, Blatt 1, Fassung Juli 1986, Korrigierter Neudruck 1990
"Systematische Berechnung hochbeanspruchter Schraubenverbindungen"

[2] Alexander, A. E.
"Analysis and design of threaded assemblies", Int. Automotive Engng. Congress and Expo- sition, Detroit, 1977, Rep. Nr. 770420

[3] Dose, G. F.; Pittner, K.-J.
"Neuartige Berechnung von Schrauben unter Berücksichtigung der Werkstoffkennwerte"
Konstruktion 48, (1996), Heft 6, Seite 183 – 188, Springer Verlag, Berlin

[4] Dose, G. F.
"Ermittlung der Scherspannungsfaktoren für die neuartige Schraubenberechnung"
Konstruktion 49, (1997). Heft 1/2, Seite 28 – 32, Springer-VDI-Verlag, Düsseldorf

[5] Dose, G. F.
"Anwendung eines Schraubenberechnungsverfahrens für weitere Gewindearten"
Konstruktion 50 (1998) Heft 7/8, Seite 71 – 75, Springer-VDI-Verlag Gmbh & Co KG, Düsseldorf